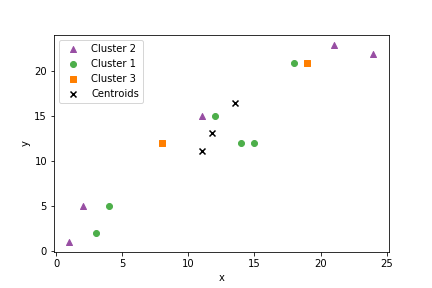
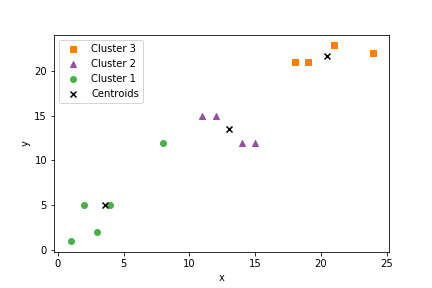
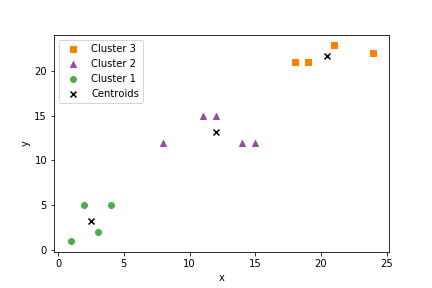
k-means clustering with Python
Today we will be implementing a simple class to perform k-means clustering with Python. Before continuing it is worth stressing that the scikit-learn package already implements such algorithms, but in my opinion it is always worth trying to implement one on your own in order to grasp the concepts better.
What is k-means clustering?
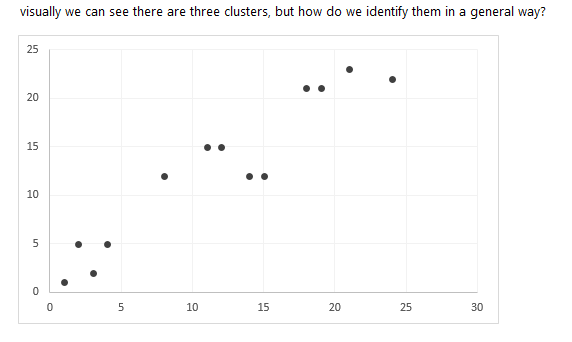
k-means clustering aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean. Imagine you have the below observations and you wanted to partition the observations and assign them to their appropriate cluster. How would you go about it? This is what we will try to put in place
Implementing the class
The algorithm will work in the following way:
- Start by assigning each point with x and y coordinates to a random cluster
- Compute the centroids of each cluster
- Re-assign each point to the closest cluster (based on the distance with the centroids)
- Repeat steps 2 and 3 until the points are not re-assigned to another cluster
Our class will have the following methods:
__init__ method:
The argument passed to our __init__ method is k, which is the number of clusters we want to identify.
1 2 3 | def __init__(self, k: int): self.k = k self.centroids = [None for _ in range(k)] |
euclidean_distance:
In order to determine the distance between two points, we will use the euclidean formula, which is:
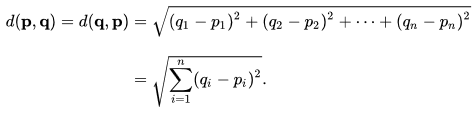
1 2 3 | @staticmethod def euclidean_distance(p1, p2): return math.sqrt(sum((x - y) ** 2 for x, y in zip(p1, p2))) |
where p1 and p2 are points with x and y coordinates, for example p1 = [10, 15], p2 = [2, 3]
_random_assign_points:
This method performs the first step of the algorithm which is to assign each point p with x and y coordinates to a random cluster
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | def _random_assign_points(self, points: list): ''' DESCRIPTION ----------------------------------- randomly assigns each point to a cluster PARAMETERS ------------------------------------ points: list of Points RETURNS ------------------------------------ a defaultdict where the keys are index from 0 to self.k - 1 and the values are the points randomly assigned to each index ''' assigned_points = defaultdict(list) for p in points: random_index = random.randrange(self.k) assigned_points[random_index].append(p) return assigned_points |
_calculate_centroids:
This method will perform step 2 which is to calculate the centroid of each cluster.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | def _calculate_centroids(self, assigned_points): ''' DESCRIPTION ----------------------------------- re-calculates the centroids based on assigned_points centroid.x = the mean of the x points of all xs centroid.y = the mean of the y points of all ys PARAMETERS ------------------------------------ assigned_points: defaultdict where the keys are the indexes from 0 to self.k-1 and the values are the points belonging to this cluster RETURNS ------------------------------------ None ''' for index, points in assigned_points.items(): # return None if no points belong to a cluster if points: self.centroids[index] = [sum(p) / len(p) for p in zip(*points)] else: self.centroids[index] = None |
_assign_points:
This method will perform step 3 which is to re-assign each point to the closest cluster based on the distance with its centroid
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | def _assign_points(self, points): ''' DESCRIPTION ----------------------------------- assigns each point in points to the cluster of its closest centroid PARAMETERS ------------------------------------ points: list of Points RETURNS ------------------------------------ defaultdict where the keys are the indexes from 0 to self.k-1 and the values are the points belonging to this cluster ''' assigned_points = defaultdict(list) for p in points: centroid_index = self._classify_point(p) assigned_points[centroid_index].append(p) return assigned_points def _classify_point(self, point): ''' DESCRIPTION -------------------------------- finds the closest centroid from P PARAMETERS -------------------------------- P = Point with x and y coordinates RETURNS ---------------------------------- Index of the closest centroid in self.centroids ''' current_min_distance = math.inf for index, centroid in enumerate(self.centroids): distance = self.euclidean_distance(point, centroid) if distance < current_min_distance: min_index = index current_min_distance = distance return min_index |
train:
This last method will make use of all the former methods and will train our data and assign each point to the appropriate cluster:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | def train(self, points: list): ''' DESCRIPTION ------------------------- Assign the points to the appropriate cluster. Steps taken: * Start by assigning each point with x and y coordinates to a random cluster * Compute the centroids of each cluster * Re-assign each point to the closest cluster (based on the distance with the centroids) * Repeat steps 2 and 3 until the points are not re-assigned to another cluster PARAMETERS ------------------------ A list of points, where each element (point) contains x and y coordinates: [4,3] or a tuple (3,1) RETURNS ----------------------- defaultdict where the keys are the indexes from 0 to self.k-1 and the values are the points belonging to this cluster. The centroids can be access by looking at the centroids attribute of the class ''' # assign points randomly to a cluster assigned_points = self._random_assign_points(points) check_assigned_points = defaultdict(list) # calculate_centroids self._calculate_centroids(assigned_points) while True: # stop when the points are not assigned to a new cluster if assigned_points == check_assigned_points: return assigned_points check_assigned_points = copy.deepcopy(assigned_points) # assign points based on the centroids assigned_points = self._assign_points(points) # recalculate centroids self._calculate_centroids(assigned_points) |
Entire class code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 | import random import math from collections import defaultdict import copy class kMeans(object): def __init__(self, k: int): self.k = k self.centroids = [None for _ in range(k)] @staticmethod def euclidean_distance(p1, p2): return math.sqrt(sum((x - y) ** 2 for x, y in zip(p1, p2))) def _classify_point(self, point): ''' DESCRIPTION -------------------------------- finds the closest centroid from P PARAMETERS -------------------------------- P = Point with x and y coordinates RETURNS ---------------------------------- Index of the closest centroid in self.centroids ''' current_min_distance = math.inf for index, centroid in enumerate(self.centroids): distance = self.euclidean_distance(point, centroid) if distance < current_min_distance: min_index = index current_min_distance = distance return min_index def _random_assign_points(self, points: list): ''' DESCRIPTION ----------------------------------- randomly assigns each point to a cluster PARAMETERS ------------------------------------ points: list of Points RETURNS ------------------------------------ a defaultdict where the keys are index from 0 to self.k - 1 and the values are the points randomly assigned to each index ''' assigned_points = defaultdict(list) for p in points: random_index = random.randrange(self.k) assigned_points[random_index].append(p) return assigned_points def _calculate_centroids(self, assigned_points): ''' DESCRIPTION ----------------------------------- re-calculates the centroids based on assigned_points centroid.x = the mean of the x points of all xs centroid.y = the mean of the y points of all ys PARAMETERS ------------------------------------ assigned_points: defaultdict where the keys are the indexes from 0 to self.k-1 and the values are the points belonging to this cluster RETURNS ------------------------------------ None ''' for index, points in assigned_points.items(): # return None if no points belong to a cluster if points: self.centroids[index] = [sum(p) / len(p) for p in zip(*points)] else: self.centroids[index] = None def _assign_points(self, points): ''' DESCRIPTION ----------------------------------- assigns each point in points to the cluster of its closest centroid PARAMETERS ------------------------------------ points: list of Points RETURNS ------------------------------------ defaultdict where the keys are the indexes from 0 to self.k-1 and the values are the points belonging to this cluster ''' assigned_points = defaultdict(list) for p in points: centroid_index = self._classify_point(p) assigned_points[centroid_index].append(p) return assigned_points def train(self, points: list): ''' DESCRIPTION ------------------------- Assign the points to the appropriate cluster. Steps taken: * Start by assigning each point with x and y coordinates to a random cluster * Compute the centroids of each cluster * Re-assign each point to the closest cluster (based on the distance with the centroids) * Repeat steps 2 and 3 until the points are not re-assigned to another cluster PARAMETERS ------------------------ A list of points, where each element (point) contains x and y coordinates: [4,3] or a tuple (3,1) RETURNS ----------------------- defaultdict where the keys are the indexes from 0 to self.k-1 and the values are the points belonging to this cluster. The centroids can be access by looking at the centroids attribute of the class ''' # assign points randomly to a cluster assigned_points = self._random_assign_points(points) check_assigned_points = defaultdict(list) # calculate_centroids self._calculate_centroids(assigned_points) while True: # stop when the points are not assigned to a new cluster if assigned_points == check_assigned_points: return assigned_points check_assigned_points = copy.deepcopy(assigned_points) # assign points based on the centroids assigned_points = self._assign_points(points) # recalculate centroids self._calculate_centroids(assigned_points) |
Using the class is easy, for example:
1 2 3 4 5 6 | if __name__ == '__main__': inputs = [[24,22],[12,15],[15,12],[1,1],[2,5],[4,5],[21,23],[14,12],[11,15],[3,2],[19,21],[18,21],[8,12]] k = kMeans(3) clusters = k.train(inputs) |
with a simple implementation in Jupyter Lab we can see visually how the clusters are formed at each iteration:
